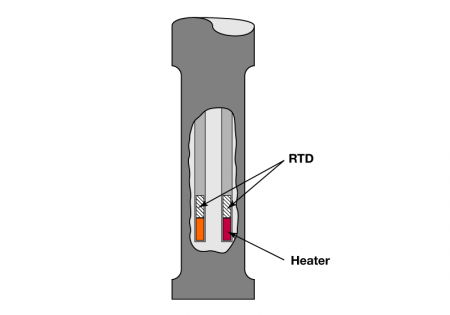
- Blending operations
- Chemical injection
- Chemical injection skids
- Chemical reactors
- Chlor-alkali process
- Deionization tanks
- Liquid-Liquid extraction
- Mixing & blending systems
- Neutralization
- Tank blanketing
- Flow: Air flow
- Flow: Centrifugal pump protection
- Flow: Compressors & Pumps
- Flow: Gas mixtures flow
- Flow: Liquified gases
- Flow: Single gas flow
- Level: Containment & drainage sumps
- Level: Lubrication oils & hydraulic fluids
- Level: Process & field storage tanks
- Level: Water storage & wash tanks
- Chemical injection
- Crude dehydration
- Crude desalting
- Production Fluid Storage
- Tank blanketing
- Vapor recovery unit
- Wellstream separation
- Chemical injection
- Chemical injection skids
- Compressor Scrubber
- Compressor Waste Liquid
- Flare Knock-out Drum
- Gas Dehydration
- NGL recovery & Storage
- Separators
- Sour gas treatment
- Sulfur Recovery
- Vapor recovery unit
- Cooling tower basins
- Cooling tower intake & basin levels
- Blending operations
- Crude desalting
- Refinery flow applications
- Condensate receiver tanks
- Cooling tower basins
- Cooling tower intake & basin levels
- Deionization tanks
- Black, green & white liquor
- Condensate receiver tanks
- Digester blow tanks
- MC pump standpipes
- Mixing & machine chests
- Pulp bleaching towers
- Pulp digesters
- Pulp storage
- Pulp washing systems
- Turpentine Recovery
- Biogas
- Geothermal
- Hydroelectric
- Solar
- Wind
- Blower air flow
- Carbon slurry level
- Digester gas flow